对于溶解效果 想必大家不会陌生 从最早的巧妙使用if判断 然后到使用step剔除等等算法 层出不穷 这里给大家分享一种简单 高效 实用的算法 并让你深入理解数学是如何在其中发挥作用 看完后你一定会说 原来看一些大佬连的加减乘除完全不懂 原来原理这么简单

首先我们做个简单的测试如下（因为是灰度图 rgb三通道数据相同 我后面就以其中一个通道数据例举了）

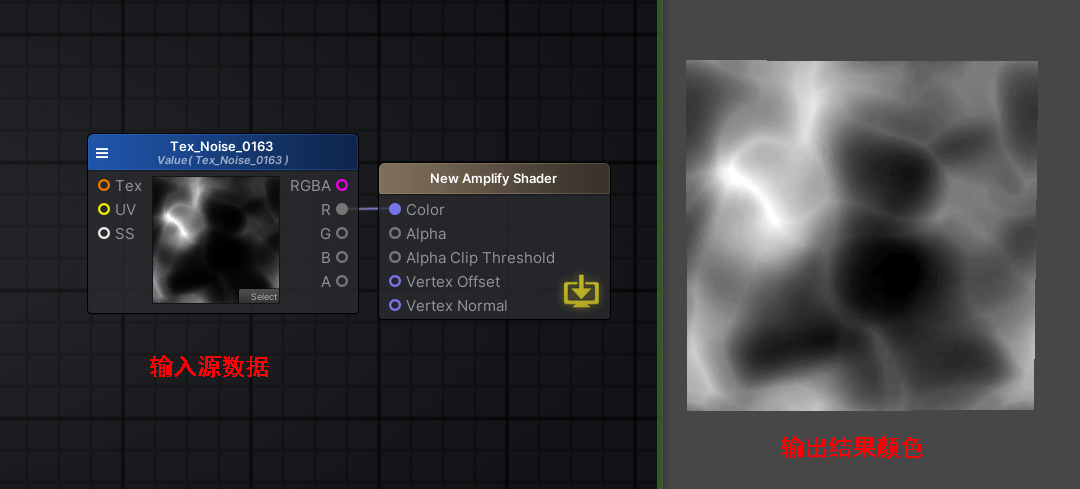
我们可以想象下 图片上有很多的点 每一个点的颜色rgba信息就是其对应的数据 数据最后又以颜色的形式输出，这个数据和颜色对应关系如下图所示(可以想象下ps里的曲线)

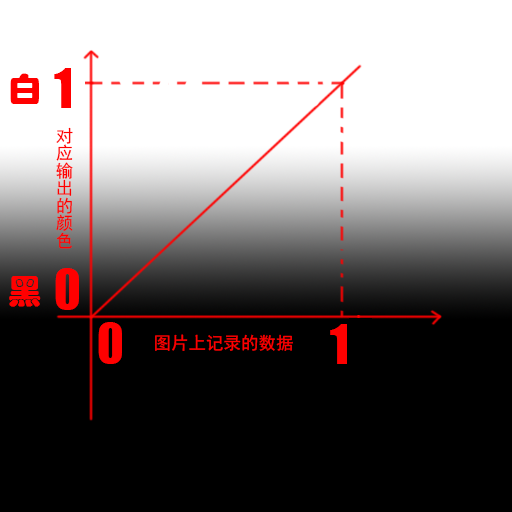
现在我们想做一个这样的变化，那就是让输入的数据小于0.1的部分全部显示为黑色，高于0.1的部分我们依旧显示为从黑到白的渐变，这样这张图片的白色像素会减少，有种溶解的感觉；

那么我们根据我们的想法重新调整下这张图，如下

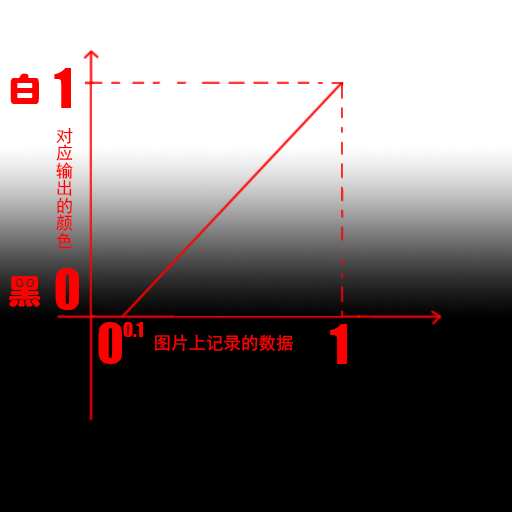
这样我们的图片还是渐变柔和的 并且将数据小于0.1的部分全部显示为了黑色（y轴小于等于零都是黑色）。到这里我们的设计思路就很清晰了，我们就是要把之前的那根直线变成下面这根直线，以达到溶解了部分像素的感觉。

下面翻出初中课本 找到两点式直线方程

（y-y2）/(y1-y2)=(x-x2)/(x1-x2)且x1不等于X2；y1不等于y2.

我们可以看到上图中的直线经过了（0.1，0）(1，1)这两个点，那么我们根据两点式带入方程（y-0)/(1-0)=(x-0.1)/(1-0.1);(0<=x<=1);简化下就是y=(x-0.1)/0.9;(0<=x<=1),这里因为我们是使用图片输入的数据，图片记得的从黑到白数据在0和1之间 所以我们的x有取值范围。

到这里数学模型就找到啦，y就代表输出的数据，x就是输入的源数据，是不是迫不及待地去测试下啦

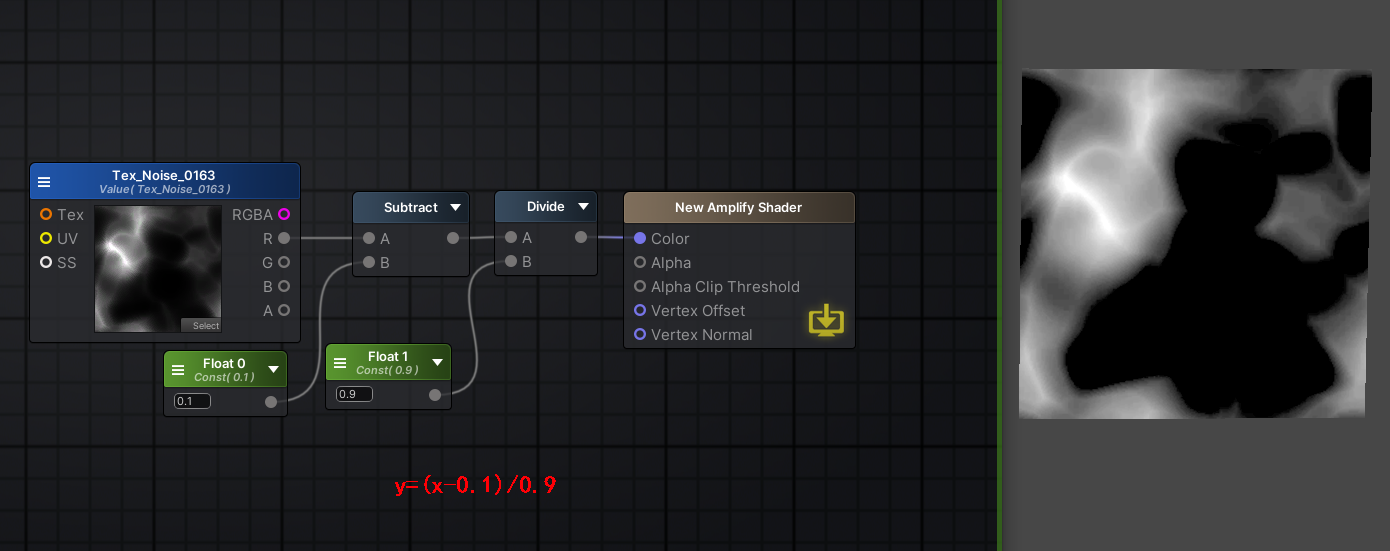
输出结果完美！就是我们想要的！

然后我们现在只是让小于0.1以下的像素变成黑色，如果这个值是个变化的呢 比如0.2，0.3等等介于0-1之间的数，这里我们假设一个变量（x1，0）其中0<=x1<=1;如图所示

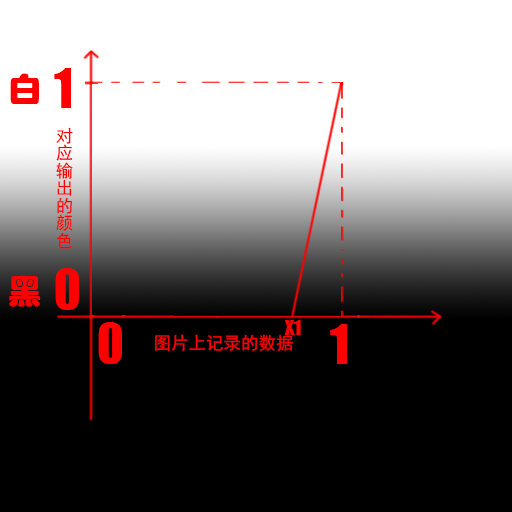
那么现在这两个点就变成了（x1，0）（1，1），重新带入公式(y-0)/(1-0)=(x-x1)/(1-x1);(0<=x1<=1;0<=x<=1),简化下就是y=(x-x1)/(1-x1);(0<=x1<=1;0<=x<=1)

继续打开ase，无脑照着方程连线就好

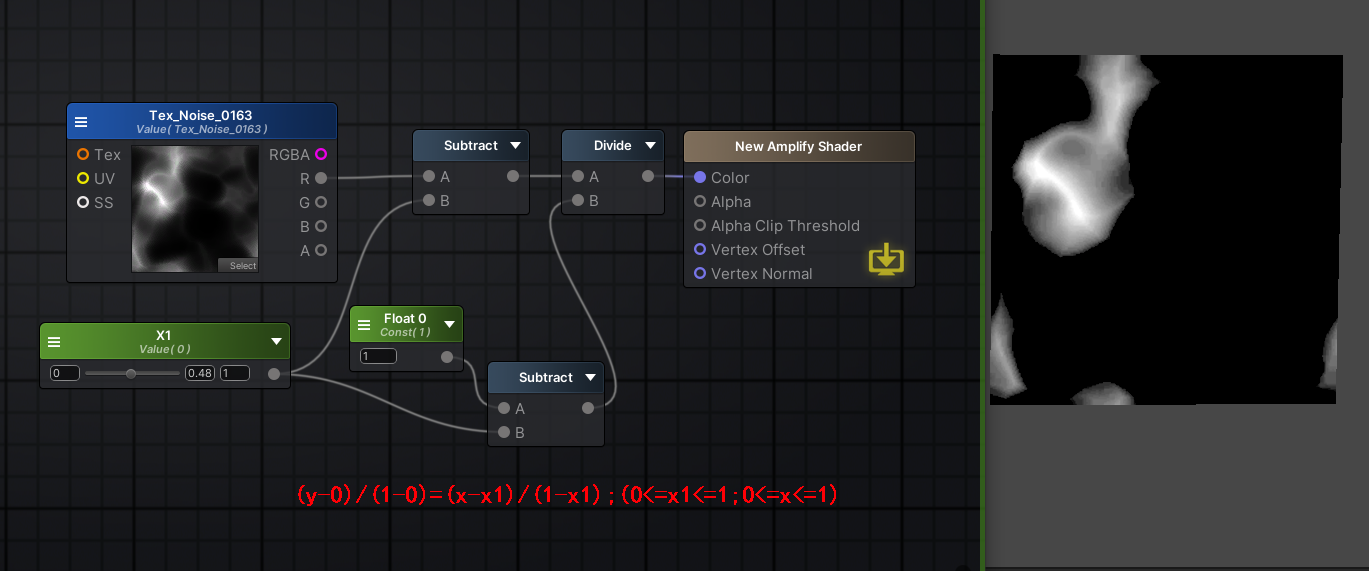
然后试着调整x1，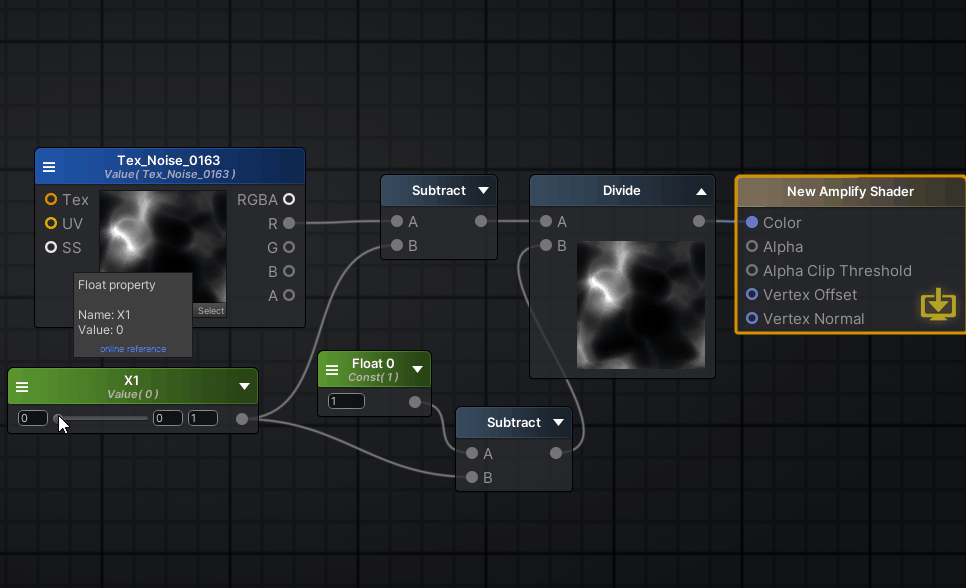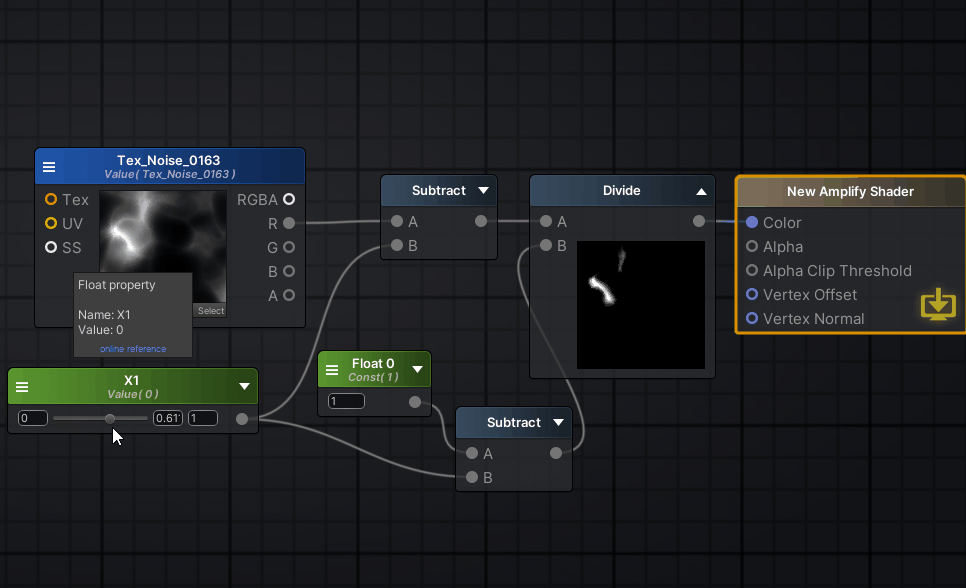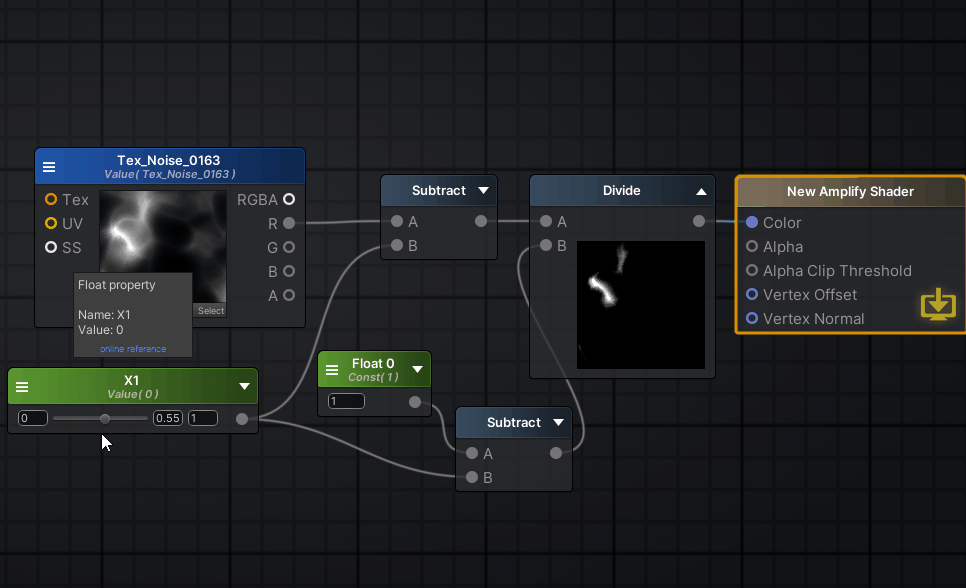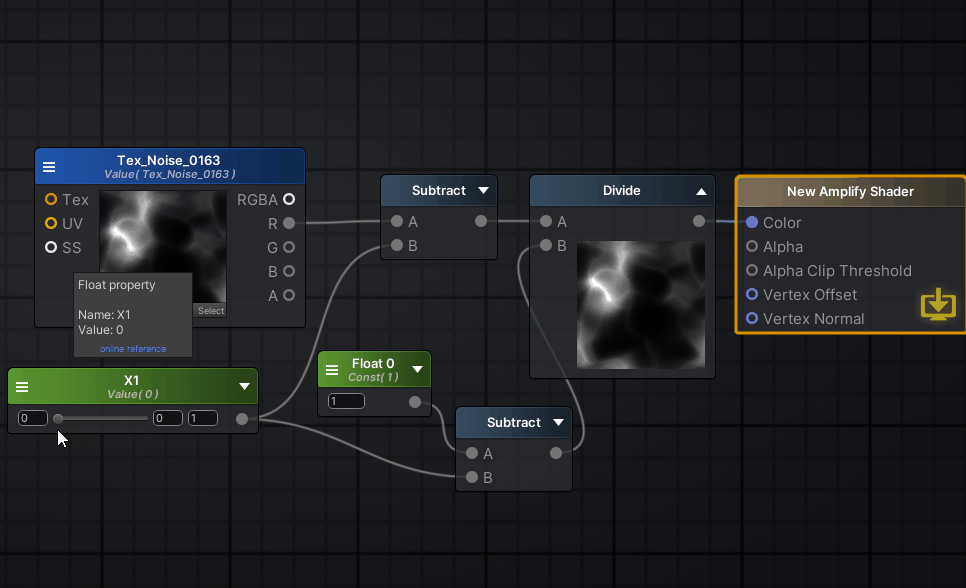

是不是之前完全看不懂的加减乘除突然豁然开朗，原来是这么回事。在此基础上的延申，还能做出很多效果或功能 这里我就不多赘述了 只是想通过这个文章让大家更多的了解数学在材质中的应用。